Rețele neurale | Daniel Volovici

COMPARAȚIE ÎNTRE METODE DE ÎNVĂȚARE DE TIP BACKPROPAGATION

Abstract: Acest articol analizează și compară diverse îmbunătățiri aduse metodei backpropagation de ajustare a ponderilor unei rețele feed-forward. Pentru aceasta se simulează comportarea rețelelor pentru 6 aplicații tipice diverse. În plus, se propune și o metodă cu pas variabil și se demonstrează prin simulare superioritatea acesteia.

1.IntroducereOrice rețea feed-forward are o structură în straturi. Fiecare strat este 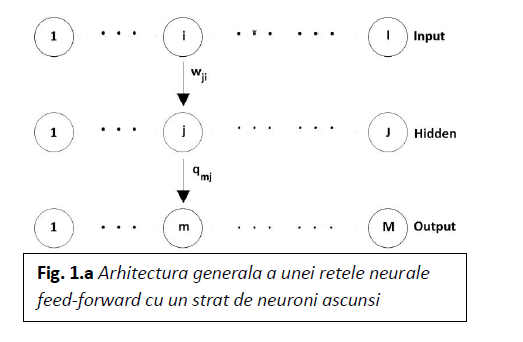compus din unități care primesc intrările de la unitățile din stratul imediat anterior și își trimit ieșirea către unitățile din stratul următor.
Regula de determinare a ponderilor sinaptice se numește regula back-propagation. Deși este posibil, nu este necesar să aplicăm această regulă la mai mult de un strat de neuroni ascunși, pentru că s-a arătat [3] că un singur strat de unități ascunse este suficient pentru a aproxima cu o anumită precizie orice funcție cu un număr finit de discontinuități, dacă unitățile ascunse au fost activate de funcții neliniare. De cele mai multe ori, în aplicații se folosește o rețea feed-forward cu un singur strat de unități ascunse și cu funcția sigmoidă de activare pentru unități.
Pentru o rețea generică cu trei straturi (figura 1.a.) starea rețelei este dată de ecuațiile:

$y_{m}=\mathfrak{F}(a_{_m});\textrm{&space;}a_{_m}=\sum_{j=1}^{J}q_{mj}\cdot v_{j}-s_{m},\textrm{&space;}m=\overline{1,M}\textrm{&space;}(1)$

$v_{j}=\mathfrak{F}(\overline{a_{j}});\textrm{ }a_{j}=\sum_{i=1}^{I}w_{ji}\cdot x_{i}-c_{j},\textrm{ }j=\overline{1,J}\textrm{ }(2)$

Ponderile sinaptice (w_ji și q_mj ) și potențialele de prag ( s_m și c_j) trebuie astfel alese încât eroarea totală:

$\mathbf{J_{s}}(\mathbf{ W,Q,s,c})=\sum_{\mu }^{ } J__{s}^{\mu }$

să fie cât mai mică. $J_{s}^{\mu }$ este eroarea pătratică la ieșire pentru patternul μ:
$\mathbf{J_{s}^{\mu}}=\frac{1}{2}\cdot \sum_{m=1}^{M}\left [ d_{m}^{\mu }-\mathfrak{F(a_{m}^{\mu })} \right ]^{2} (4)$

unde d^μ este vectorul ieșire dorit pentru clasa μ . Se observă deci că regula back-propagation este o generalizare a regulii delta. În consecință, trebuie să calculăm gradientul lui J, în raport cu fiecare parametru și apoi să modificăm proporțional cu acest gradient valoarea respectivului parametru. În prima fază considerăm numai conexiunile sinaptice ale neuronilor de ieșire:
$\Delta q_{mj}= -\rho \cdot \frac{\partial J_{s}}{\partial q_{mj}}=-\rho \cdot \sum_{\mu}^{ }\frac{\partial J_{s}^{\mu }}{\partial q_{mj}}\cdot \frac{\partial a_{m}^{\mu }}{\partial q_{mj}} =\rho \cdot \sum_{\mu}^{ }[d_{m}^{\mu }-\mathfrak{F(a_{m}^{\mu })}]\cdot \mathfrak{F(a_{m}^{\mu })}\cdot \frac{\partial a_{m}^{\mu }}{\partial q_{mj}}\equiv \rho \cdot \sum_{\mu}^{ }\Delta _{m}^{\mu \cdot V_{j}^{\mu }} (5))$

$\Delta S_{m}= -\rho \cdot \frac{\partial J_{s}}{\partial J_{m}}=\rho \cdot \sum_{\mu}^{ }[d_{m}^{\mu }-\mathfrak{F(a_{m}^{\mu })}]\cdot \mathfrak{F(a_{m}^{\mu })}\cdot \frac{\partial a_{m}^{\mu }}{\partial S_{m}}=- \rho \cdot \sum_{\mu}^{ }\Delta _{m}^{\mu }= \rho \cdot \sum_{\mu}^{ }\Delta _{m}^{\mu }\cdot (-1)$

$\small \Delta _{m}^{\mu }=[d_{m}^{\mu }-\mathfrak{F(a_{m}^{\mu })}]\cdot \mathfrak{F(a_{m}^{\mu })} (7)$

În pasul următor considerăm parametrii asociați cu conexiunile sinaptice dintre stratul de intrare și cel ascuns. Procedura este asemănătoare, numai că trebuie făcute două substituții:

$\Delta w_{ji}=-\rho \cdot \frac{\partial J_{s}}{\partial w_{ji}}=-\rho \cdot \sum_{\mu }^{ }\sum_{m=1}^{M}\frac{\partial J_{s}^{\mu }}{\partial a_{m}^{\mu }}\cdot \frac{{\partial a_{m}^{\mu }}}{\partial v_{j}}\cdot \frac{\partial v_{j}}{\partial w_{ji}}=\rho \cdot \sum_{\mu }^{ }\sum_{m=1}^{M}[d_{m}^{\mu }-\mathfrak{F(a_{m}^{\mu })}]\cdot \mathfrak{F(a_{m}^{\mu })}\cdot\frac{{\partial a_{m}^{\mu }}}{\partial v_{j}}\cdot \frac{\partial v_{j}}{\partial w_{ji}}=\rho \cdot \sum_{\mu }^{ }\sum_{m=1}^{M}\Delta _{m}^{\mu }\cdot q_{mj}\cdot \mathfrak{F}(\overline{a_{J}^{\mu }})\cdot \frac{\partial\overline{ a_{J}}}{\partial w_{ji}}\equiv \rho \cdot \sum_{\mu }^{ } \overline{\Delta _{J}^{\mu }}\cdot x_{i}^{\mu } (8)$

$\Delta c_{j}=-\rho \cdot \frac{\partial J_{s} }{\partial c_{j}}\equiv -\rho\cdot \sum_{\mu }^{ }\overline{\Delta _{J}^{\mu }}= \rho\cdot \sum_{\mu }^{ }\overline{\Delta _{J}^{\mu }}\cdot (-1) (9)$

unde:

$\overline{\Delta _{J}^{\mu }}=\left [ \sum_{m}^{ }\Delta _{m}^{\mu }\cdot q_{mj} \right ]\cdot \mathfrak{F(\overline{a_{j}^{\mu }})}(10)$

De observat că ecuațiile de ajustare a ponderilor sinaptice (8) și (9) au aceeași formă cu ecuațiile sinaptice (5) și (6), numai expresia lui $\overline{\Delta _{J}^{\mu }}$ diferă de $\Delta _{m}^{\mu }$ , din care se poate obține recursiv.
Metoda backpropagation a fost extinsă și la rețelele recurente [11, 12, 13], care din acel moment au devenit tot mai populare.
Schema de corecție a erorilor lucrează ca și cum informația despre abaterea de la ieșirea dorită s-ar propaga înapoi (backward) prin rețea, ”contra curentului” conexiunilor sinaptice. Este îndoielnic, cu toate că nu complet imposibil, ca o asemenea procedură să poată fi realizată de rețelele neurale biologice. Ceea ce este sigur, este că algoritmul propagării înapoi a erorii este foarte potrivit pentru calculatoarele electronice, atât în implementările hardware, cât și software. Mai recent, s-a produs și o regulă de tip ”backpropagation” care se bazează nu pe minimizarea erorii pătratice medii totale, ci pe maximizarea informației Küllbach [2].

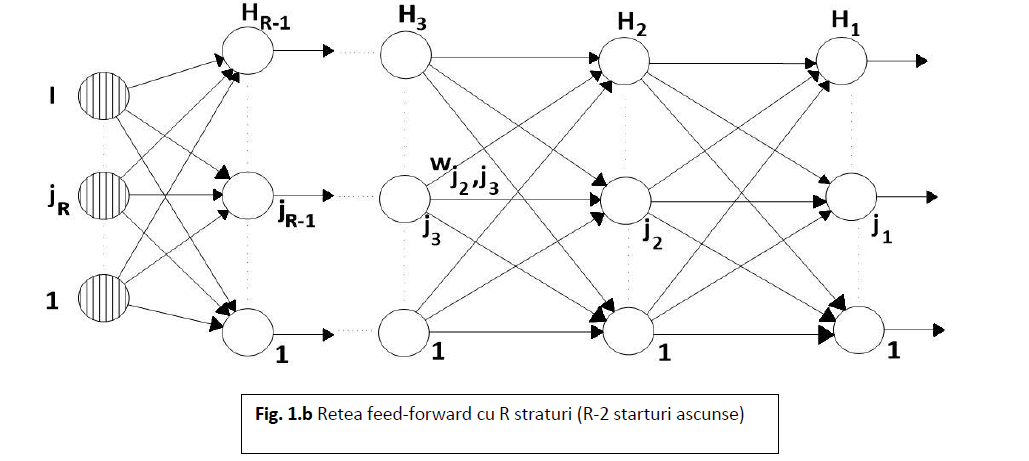
Arhitectura din figura 1.a. ca și relațiile (5)-(10) pot fi generalizate la o rețea feedforward cu R straturi (R-2 straturi ascunse) obținând arhitectura din figura1.b. Criteriul de eroare care trebuie minimizat este tot eroarea medie pătratică determinată pe mulțimea tuturor exemplelor de antrenament:
$J=\sum_{\mu }{ }\sum_{j_{1}}^{H_{1}}(d_{j_{1}}^{\mu }-v_{j_{1}}^{\mu })^{2} (11)$

Ieșirea rețelei va fi tocmai ieșirea ultimului strat neuronal:

$v _{j_{c}}^{\mu }=\mathfrak{F}\left ( \sum_{j_{c+1}=1}^{H_{c+1}} w_{j_{c},j_{c+1}}\cdot v _{j_{c+1}}^{\mu }-s_{j_{c}} \right )(12)$

Aplicând regula backpropagation se obțin următoarele relații:

$\Delta w_{j_{c},j_{c+1}}=\sum_{\mu }^{ }\Delta_{j_{c}}^{\mu } \cdot v _{j_{c+1}}^{\mu }(13)$

$\Delta _{j_{c}}^{\mu }=\left ( \sum_{j_{c-1}=1}^{H_{c-1}}\Delta _{j_{c-1}}\cdot w_{j_{c-1}j_{c}}\right )\cdot \mathfrak{F}\left ( v_{j_{c}}^{\mu } \right )(14)$

$\Delta _{j_{1}}^{\mu }= \sum_{j_{1}=1}^{H_{1}} \left ( d_{j_{1}}^{\mu }-v_{j_{1}}^{\mu } \right )\cdot \mathfrak{F}\left ( v_{j_{1}}^{\mu } \right )(15)$

$\Delta S_{j_{c}}=\sum_{\mu }^{ }\Delta_{j_{c}}^{\mu } \cdot (-1)(16)$

Metoda backpropagation fiind o metodă de minimizare a erorii medii pătratice pe întreaga mulțime a exemplelor de antrenament, metodă bazată pe gradientul negativ, suferă de deficiențele generale ale tehnicilor de gradient. Aceste deficiențe sunt, în general, două:

Rata de învățare, ρ, care dă mărimea pasului pe direcția gradientului trebuie să fie suficient de mică. Aceasta deoarece gradientul este o măsură locală, iar dacă este prea mare s-ar putea ca măsura J a erorii să nu scadă, ci doar să oscileze, vectorul coeficienților sinaptici sărind de pe o parte pe cealaltă a ”gropii” în care se găsește minimul local. Pe de altă parte, un ρ prea mic conduce la o viteză prea mică de convergență, ceea ce conduce la o învățare prea lentă. Chiar dacă se poate determina (cu mare consum de timp) un ρ optim, acest optim se modifică pe măsură ce sistemul învață; de asemenea el diferă de la problemă la problemă.
Indiferent de cât de rapid atinge minimul, acesta va fi minimul local cel mai apropiat și din acesta nu va putea ieși pentru că tehnica backpropagation, fiind o metodă de gradient, este o metodă ce exploatează proprietățile locale ale funcției criteriu. În plus, se poate deduce: cu cât dimensiunea spațiului de căutare (spațiul ponderilor) este mai mare (deci avem un număr mai mare de neuroni în straturile ascunse), cu atât crește numărul minimelor locale și deci și ”șansa” de a eșua într-unul dintre acestea.

Cu aceste perspective vom compara metoda backpropagation clasică cu unele dintre îmbunătățirile prezentate în literatură și, în final, vom propune o metodă care să conveargă mai rapid și să poată evada din minimele locale.

Pentru aceasta vom simula comportarea rețelelor respective în rezolvarea a 6 probleme tipice.

2.Problemele la a căror rezolvare s-au testat metodele

Pentru fiecare problemă se va specifica numărul de unități de intrare, de ieșire și din stratul ascuns. Pentru determinarea numărului de unități din acest strat se va ține cont de rezultatul altor simulări [17] unde se stabilește empiric faptul că, pentru a putea rezolva problemele de clasificare este bine ca acest număr să fie aproximativ egal cu media aritmetică dintre numărul neuronilor de intrare și numărul celor de ieșire, dar nu mai mic decât 10.
2.1. BINAR

Această problemă constă în determinarea parității unui cuvânt de 8 biți (EXCLUSIVE-OR Task) [6,9].

Rețelele folosite vor avea deci 8 unități de intrare și una de ieșire care va lua valoarea 0 pentru un cuvânt cu un număr par de biți de 1 și valoarea 1 în caz contrar. Numărul de unități ascunse este egal cu 10.
În această problemă am ales antrenarea rețelei pe mulțimea tuturor exemplelor posibile, deci pe 256 de exemple.

2.2. COUNTER

Se propune realizarea unui numărător de biți de 1 dintr-un cuvânt binar de 4 biți [6,9]. Deci, vom avea 4 neuroni de intrare și 5 de ieșire, vectorul ieșirilor aparținând mulțimii {(1,0,0,0,0)^T,(0,1,0,0,0)^T, (0,0,1,0,0)^T (0,0,0,1,0)^T (0,0,0,0,1)^T} fiind egal cu vectorul i (i=1, … , 5) dacă vectorul de intrare are i-1 biți de 1. Numărul ales pentru unitățile ascunse este 10. Am antrenat rețelele pe toate exemplele de antrenament posibile; așadar, numărul acestora este 2⁴ = 16.

2.3. MULTIPLEXOR

Rețeaua neurală care îl va simula trebuie să învețe ca vectorului de intrare de 3 biți (3 neuroni de intrare) (b₁,b₂,b₃)^T să-i atașeze la ieșire vectorul de 8 biți (0,0,..,0,1,0,…,0)^T cu un singur 1 în poziția i =b₁ •2² +b_2• 2 + b₃. Numărul exemplelor de antrenament este 2³=8 [6], iar numărul unităților ascunse este, evident, tot egal cu 10

2.4. 5x5 TABLE

Această problemă este problema recunoașterii (clasificării) liniilor și coloanelor într-o figură binară. Imaginea este reprezentată de o rețea de 5×5 (5 linii și 5 coloane, adică 25 de celule de intrare, respectiv 25 de neuroni de intrare). Deoarece fiecare imagine poate conține atât linii cât și coloane vom avea 2 neuroni de ieșire; numărul neuronilor din stratul ascuns l-am ales egal cu 14.
Considerând imaginea dată de matricea C_[n,m] , (n, m, = 1, … , 5), atunci vectorii de intrare x[i] se vor forma luând i = 3·(n-1)+m. Am ales simularea învățării pentru o mulțime de 16 exemple, pentru fiecare dând ca în orice învățare supervizată și vectorul de ieșire dorit d:

x                                                                                        d
11111.00000.00000.00000.00000                                                              1 0
00000.11111.00000.00000.00000                                                              1 0
00000.00000.11111.00000.00000                                                              1 0
00000.00000.00000.11111.00000                                                              1 0
00000.00000.00000.00000.11111                                                              1 0
10000.10000.10000.10000.10000                                                              0 1
01000.01000.01000.01000.01000                                                              0 1
00100.00100.00100.00100.00100                                                              0 1
00010.00010.00010.00010.00010                                                              0 1
00001.00001.00001.00001.00001                                                              0 1
11111.11111.00000.00000.00000 1 0
00000.00000.00000.11111.11111 1 0
11000.11000.11000.11000.11000 0 1
00011.00011.00011.00011.00011 0 1
10000.01000.00100.00010.00001                                                           1/2 1/2
00001.00010.00100.01000.10000                                                           1/2 1/2

2.5. ASSOCIATIVE MEMORY

Se testează capacitatea de ”feature extraction” a rețelelor neurale, adică posibilitatea de a reține ”formele” de intrare intr-un vector de dimensiune mică. Prin urmare, rețeaua e învățată ca unui vector de intrare de 16 biți să-i corespundă același vector (tot de 16 biți) la ieșire [9,10]. Dificultatea constă în aceea că stratul ascuns are numai 4 neuroni. Am antrenat rețelele pe o mulțime de 16 exemple: vectorii cu a i-a componentă egală cu 1 (i = 1, … , 16), iar celelalte componente egale cu 0.

2.6. FUNCTION

Pe lângă rețelele recurente (capabile să reprezinte serii de timp) se folosesc la emularea proceselor și rețele feedforward, conectate în arhitectura din figura 2.a. [14, 15].

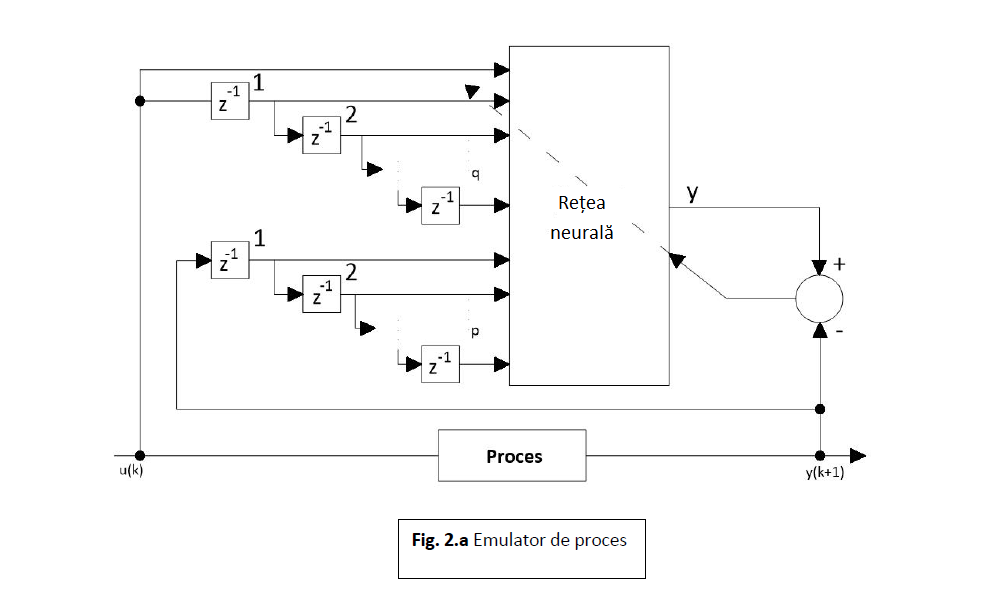
Fiind dați p și q se poate emula un proces cu o rețea neurală cu m=p+q+1 intrări și o ieșire. Notând reprezentarea realizată de emulator prin φ_E( •) și ieșirea lui prin y’ avem:

$y'=\varphi_{E} (X_{E})(17)$

unde:

$x_{E}(k)=[y(k),y(k-1),...,y(k-p+1),u(k),u(k-1),...,u(k-q)]^{T}(18)$

Emulatorul este antrenat să minimizeze măsura erorii de emulare: y(k+1)-y’. În figura 2.a., prin z^-1 se înțelege operatorul de întârziere.
Pentru testarea metodelor de învățare am ales un sistem de ordinul doi profund neliniar, care a fost folosit în [5] și care îl preia din [8]. Sistemul este descris de ecuația:

$y(k)=\frac{y(k-1)\cdot y(k-2)\cdot [y(k-1)+2,5]}{1+y^{2}(k-1)+y^{2}(k-2)}+u(k)(19)$

unde u(k) este un semnal sinusoidal:

$u(k)=sin(0,08\cdot \pi \cdot k)(20)$

Am generat 80 de perechi (u(k), y(k)), pornind de la y(-1)=0 și y(0)=1 și le-am folosit pentru antrenarea off-line a rețelelor.
Așa cum se procedează în general, am presupus cunoscut ordinul procesului SISO (Single Input Single Output) și, de aceea, am ales o rețea cu 3 unități de intrare, o unitate de ieșire și 10 unități ascunse. Unitățile de intrare se conectează ca în figura 2.b. și anume, la momentul k, cele trei unități x vor fi legate câte una la y(k-2), y(k-1) și u(k), în timp ce ieșirea dorită, d, va fi considerată y(k).

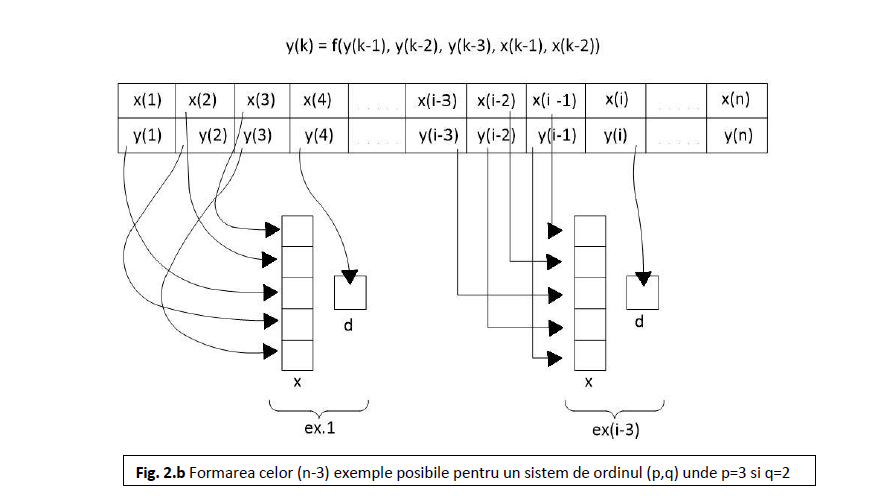
De fapt, deoarece ieșirea unui neuron este cuprinsă întotdeauna între 0 și 1, trebuie efectuată o conversie a valorii lui y în acest interval. Am ales o transformare liniară a domeniului în care ia valori y în intervalul (0.15, 0.85) pentru a permite adaptarea rețelei și la semnale care ulterior perioadei de învățare ar ieși din plaja de valori de antrenament și, apoi, pe MaxDy care este modulul abaterii valorilor de la medie, de unde rezultă:

$d(k)=\frac{1}{2}+0,7\cdot \frac{|y(k)-Medy|}{MaxDy}(21)$

Spre deosebire de alți autori, nu efectuez o operație asemănătoare și pentru intrări: o asemenea operație ar ușura poate adaptarea, dar ar complica arhitectura pentru antrenament căci ar trebui să se facă o distincție între tipurile de intrări (care provin din intrările procesului și care din ieșirile acestuia).

3. Metodele de învățare
3.1. BackPropagation Classic (BP)
La metoda clasică rămâne la alegerea utilizatorului precizarea valorii ratei de învățare, adică a mărimii pasului în direcția gradientului funcției criteriu J. Așa cum am arătat în paragraful 1, această valoarea nu trebuie să fie nici prea mare, nici prea mică. Până acum nu s-a elaborat o metodă universală de alegere a lui ρ într-o problemă dată. Se recomandă ca ρ să fie subunitar sau, eventual, descrescător odată cu creșterea numărului iterației.
S-a arătat că viteza de scădere a funcției criteriu depinde foarte puternic de valoarea aleasă pentru ρ. În general se recomandă să se testeze evoluția rețelei pentru diverse valori ale lui ρ și apoi să se aleagă o valoarea convenabilă. Se poate porni cu o valoare relativ mică pentru ρ și să se crească această valoare, atât timp cât prin această creștere scade J. În momentul în care ρ depășește valoarea optimă și devine prea mare apar oscilații ale valorii lui J, care uneori crește în loc să scadă.
Noi am testat comportarea rețelei pentru diverse valori ale lui ρ alegând valoarea optimă.
Totuși nu numai ρ este neprecizat, așa cum părea la prima vedere, ci și valorile inițiale ale ponderilor rețelei. Acestea se aleg aleatoriu în intervalul [-1, 1]. În concluzie, ar fi greșit să se aleagă ρ pentru un oarecare set de ponderi. De aceea am simulat comportarea fiecărei rețele, pentru fiecare ρ, în cazul a 10 seturi diferite de ponderi inițiale. Este evident că, pentru o aceeași problemă, indiferent de metoda de învățare și de parametrii variabili, am luat de fiecare dată aceleași 10 seturi de ponderi aleatorii inițiale.
Fiecare metodă am rulat-o același timp. De asemenea, deoarece iterațiile nu durează un timp egal chiar la aceeași metodă, am reprezentat pe abscisă în graficele din figura 3 timpul de rulare (2 minute pe un PC-IBM 486; 50 MHz: dar acest timp este neesențial la compararea metodelor).
Pe ordonată am reprezentat logaritmul zecimal al funcției criteriu J pentru întreaga mulțime a exemplelor. Am ales reprezentarea la scară logaritmică pentru că erorile ajung oricum la valori mult mai mici decât cele inițiale, dar contează ordinul de mărime al acestora la diverse momente de timp.
Fiecare linie de 3 grafice prezintă pe scurt rezultatele simulărilor în cazul unei probleme. Graficul din stânga prezintă $lg \underset{i=1,10}{\underline{max}}J_{i}(t;\rho )$ , unde i este setul de ponderi inițiale pentru un ρ dat la fiece moment de timp t. Graficul din dreapta este al funcțiilor $lg \underset{i=1,10}{\underline{min}}J_{i}(t;\rho )$ , iar cel din mijloc este $\lg \left [ \frac{1}{10}\cdot \sum_{i=1}^{10}J_{i}(t;\rho ) \right ]$ , deci corespunde mediei funcțiilor criteriu pentru un anume ρ.
Pentru a alege valoarea optimă a lui ρ comparăm curbele logaritmului mediilor (graficul din mijloc), iar în cazul mai multor valori cu rezultate asemănătoare, ne vom ghida și după celelalte grafice. Din motive de claritate a desenului nu am desenat curbele pentru toate valorile ρ pentru care am efectuat simulările.
S-au efectuat următoarele simulări:
1). BINAR: ρ=0.1 (curbele 1); ρ=0.18; ρ=0.26 (curbele 2); ρ=0.3; ρ=0.34 (curbele 3);
ρ=0.38; ρ=0.42 (curbele 4); ρ=0.5.
Cel mai bun rezultat: ρ=0.34 (curbele 3).
2). COUNTER: ρ=0.1; ρ=0.18 (curbele 1); ρ=0.26; ρ=0.34 (curbele 2); ρ=0.42; ρ=0.5
(curbele 3); ρ=0.58; ρ=0.66 (curbele 4).
Cel mai bun rezultat: ρ=0.5 (curbele 3).
3). MULTIPLEXOR: ρ=0.1; ρ=0.18; ρ=0.26; ρ=0.34; ρ=0.42 (curbele 1); ρ=0.5; ρ=0.58;
ρ=0.66 (curbele 2); ρ=0.74; ρ=0.82; ρ=0.9 (curbele 3); ρ=0,98; ρ=1.06;
ρ=1.14; ρ=1.22 (curbele 4); ρ=1.3.
Cel mai bun rezultat: ρ=1.22 (curbele 4).
4). 5×5 TABLE: ρ=0.1 (curbele 1); ρ=0.18 (curbele 2); ρ=0.26; ρ=0.34 (curbele 3); ρ=0.42;
ρ=0.5; ρ=0.58 (curbele 4); ρ=0.66.
Cel mai bun rezultat: ρ=0.58 (curbele 4).

5). ASSOCIATIVE MEMORY: ρ=0.1 (curbele 1); ρ=0.18 (curbele 2); ρ=0.26; ρ=0.34;
(curbele 3); ρ=0.42; ρ=0.5 (curbele 4); ρ=0.58.
Cel mai bun rezultat: ρ=0.5 (curbele 4).
6). FUNCTION: ρ=0.01 (curbele 1); ρ=0.02 (curbele 2); ρ=0.04; ρ=0.06 (curbele 3); ρ=0.1;
(curbele 4); ρ=0.18.
Cel mai bun rezultat: ρ=0.02 (curbele 2).
3.2. BackPropagation with Term Proportion (BPTP)
Deoarece, în general, convergența este lentă la regula backpropagation, s-au propus diverse îmbunătățiri ale algoritmului de modificare a ponderilor. La algoritmul backpropagation, procedura de învățare necesită o modificare a ponderilor cu $\frac{ \partial J_{s}^{\mu} }{\partial w}$ . Metoda gradientului negativ impunea luarea de pași infinitezimali, constanta de proporționalitate fiind rata învățării, ρ. Din motive practice, de convergență mai rapidă, alegem o rată de învățare cât mai mare fără a ajunge la oscilații.
O cale de evitare a oscilațiilor la valori mari ale lui ρ este de a modifica ponderea în funcție și de modificarea anterioară, prin adăugarea unui termen proporție:
$\Delta w_{ji}(k+1)=\rho \cdot \Delta _{j}^{\mu}\cdot x_{i}^{\mu }+\beta \cdot \Delta w_{ji}(k))(22)$
unde k este numărul iterației și β este o constantă pozitivă.
În literatură se afirmă că prin adăugarea termenului proporție, minimul se obține mai rapid pentru că sunt permise rate mai mari de învățare fără a avea oscilații. De asemenea se recomandă [7] ca β=ρ/k.
Pentru a testa aceste afirmații am antrenat rețelele pentru fiecare problemă pentru care am testat regula clasică pornind de la aceleași 10 seturi de ponderi inițiale ale fiecărei probleme.
La fiecare problemă am crescut valoarea lui ρ găsită optimă cu algoritmul BP până când apăreau oscilații, determinând astfel ρ optim și pentru acest algoritm.
Am rulat în fiecare caz același timp ca și în algoritmul BP, deși, fiind necesare mai multe calcule, numărul de iterații era mai mic, acesta fiind tributul plătit pentru creșterea complexității algoritmului.
Rezultatul simulărilor sunt sintetizate în figura 4, unde aranjarea graficelor este aceeași ca și în figura 3:
1). BINAR: ρ=0.3 (curbele 3); ρ_BP=0.34 (curbele 1); ρ_BP=0.38 (curbele 2); ρ=0.42.
Cel mai bun rezultat: ρ=0.38 (curbele 2).
2). COUNTER: ρ=0.42 (curbele 1); ρ_BP=0.5 (curbele 2); ρ=0.58 (curbele 3).
Cel mai bun rezultat: ρ=0.5 (curbele 2).
3). MULTIPLEXOR: ρ=0.9; ρ=0.98 (curbele 3); ρ=1.06; ρ=1.14; ρ_BP=1.22 (curbele 2); ρ=1.3 (curbele 1).
Cel mai bun rezultat: ρ=0.98 (curbele 3).
4). 5×5 TABLE: ρ_BP=0.58 (curbele 1); ρ=0.66 (curbele 2); ρ=0.74 (curbele 3); ρ=0.82.
Cel mai bun rezultat: ρ=0.74 (curbele 3).
5). ASSOCIATIVE MEMORY: ρ=0.34; ρ=0.42 (curbele 1); ρ_BP=0.5 (curbele 2); ρ=0.58 (curbele 3).
Cel mai bun rezultat: ρ=0.42 (curbele 1).
6). FUNCTION: ρ=0.01 (curbele 1); ρ_BP=0.02 (curbele 2); ρ=0.04 (curbele 3).
Cel mai bun rezultat: ρ=0.02 (curbele 2).

3.3 BackPropagation with Term Proportion and Restart (BPTPR)
Pentru a asigura convergența algoritmului BPTP am luat β=ρ/k și, după un număr mare de iterații, β devine atât de mic încât termenul proporție nu mai are nicio contribuție la variația ponderilor. De aceea s-a propus introducerea unui restart în sensul că se ”restartează” periodic direcția de modificare a ponderilor la direcția gradientului. Astfel:
$\beta _{k}=\left\{\begin{matrix} \rho /i \: \: pentru \: i\neq 0\\0\: \: \: \; \: \: pentru \: i=0 \end{matrix}\right.\; \; unde i=k\: mod\: I\; (23)$
Pentru I=1 metoda se reduce la BPTP. Se recomandă ca I să ia valori între 2 și 10.
De data aceasta avem două variabile: ρ și I. Presupunând că valoarea optimă a lui ρ nu se schimbă prea mult față de metoda anterioară, se caută valoarea optimă a lui I ținând ρ=ρ_{optim BPTP} pentru fiecare problemă în parte, după care fixând pe I, verificăm optimul lui ρ în jurul valorii ρ_{optim BPTP}.
Efectuând simulările în aceleași condiții ca și la metodele anterioare obținem rezultatele prezentate sintetic în figura 5:
1). BINAR: ρ_BPTP=0.38 și I=3; ρ_BPTP=0.38 și I=5 (curbele 1);
ρ_BPTP=0.38 și I=6 (curbele 2);
ρ_BPTP=0.38 și I=7 (curbele 3);
ρ_BPTP=0.38 și I=10; I=6 și ρ=0.34; I=6 și ρ=0.42 (curbele 4); I=6 și ρ=0.46;
Cel mai bun rezultat: ρ=0.42 și I=6 (curbele 4).
2). COUNTER: ρ_BPTP=0.5 și I=3 (curbele 1);
ρ_BPTP=0.5 și I=4 (curbele 2);
ρ_BPTP=0.5 și I=5 (curbele 3);
I=4 și ρ=0.34; I=4 și ρ=0.42 (curbele 4); I=4 și ρ=0.58;
Cel mai bun rezultat: ρ=0.42 și I=4 (curbele 4).
3). MULTIPLEXOR: ρ_BPTP=0.98 și I=2 (curbele 1);
ρ_BPTP=0.98 și I=3 (curbele 2);
I=2 și ρ=0.9 (curbele 3);
I=2 și ρ=1.06 (curbele 4).
Cel mai bun rezultat: ρ=0.98 și I=2 (curbele 1).
4). 5×5 TABLE: ρ_BPTP=0.74 și I=2; ρ_BPTP=0.74 și I=3 (curbele 1);
ρ_BPTP=0.74 și I=4; ρ_BPTP=0.74 și I=5 (curbele 2);
ρ_BPTP=0.74 și I=6; ρ_BPTP=0.74 și I=7 (curbele 3);
I=5 și ρ=0.66; I=5 și ρ=0.82 (curbele 4).
Cel mai bun rezultat: ρ=0.74 și I=5 (curbele 2).
5). ASSOCIATIVE MEMORY: ρ_BPTP=0.42 și I=2 (curbele 1);
ρ_BPTP=0.42 și I=3 (curbele 2);
I=2 și ρ=0.34 (curbele 3);
I=2 și ρ=0.5 (curbele 4).
Cel mai bun rezultat: ρ=0.42 și I=2 (curbele 1).
6). FUNCTION: ρ_BPTP=0.02 și I=2 (curbele 1);
ρ_BPTP=0.02 și I=3 (curbele 2);
ρ_BPTP=0.02 și I=4 (curbele 3);
ρ_BPTP=0.02 și I=5; I=3 și ρ=0.01; I=3 și ρ=0.04 (curbele 4).
Cel mai bun rezultat: ρ=0.02 și I=3 (curbele 4).

3.4. Conjugate Gradient BackPropagation (CGBP)
O altă idee a fost aplicarea tehnicilor aprofundate în teoria optimizării. De fapt, se observă că BPTPR este o variantă simplificată a metodei gradienților conjugați cu restart. Metoda gradienților conjugați cu restart diferă de BPTPR numai prin alegerea lui β, care aici se calculează mai complicat, în funcție de norma gradientului de la iterația actuală, k, și de la iterația precedentă, k-1, după formula:
$\beta _{k}=\left\{\begin{matrix} \frac{g_{i}}{g_{i-1}}\cdot \frac{g_{i}-g_{i-1}}{g_{i-1}}\; pentru \: i\neq 0\\ 0 \; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; pentru \: i=0 \end{matrix}\right. unde\; i - k\: mod \: I\: \; (24)$
Totuși, și la această metodă trebuie ales coeficientul ρ și indicele de restart I. De aceea am reluat simulările cu scopul de a determina valorile optime ale lui ρ și I. Pentru început se menține constantă valoarea lui ρ (ρ=ρ_{optim BPTPR}) și se caută valoarea optimă a lui I în jurul valorii I_{optim BPTPR}. Apoi fixăm pe I la I_{optim CGBP} și căutăm ρ_{optim CGBP} în jurul lui ρ_{optim BPTPR}.
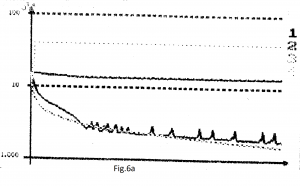
S-au efectuat următoarele simulări (figura 6):
1). BINAR: ρ_BPTPR=0.42 și I=5 (curbele 1); ρ_BPTPR=0.42 și I_BPTPR= 6; ρ_BPTPR=0.42 și I=7;
ρ_BPTPR=0.42 și I=8 (curbele 2);
ρ_BPTPR=0.42 și I=9; ρ_BPTPR=0.42 și I=10; ρ_BPTPR=0.42 și I=11 (curbele 3);
I=11 și ρ=0.34; I=11 și ρ=0.5 (curbele 4).
Cel mai bun rezultat: ρ=0.42 și I=11 (curbele 3).
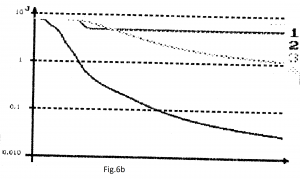
2). COUNTER: ρ_BPTPR=0.42 și I=3 (curbele 1);
ρ_BPTPR=0.42 și I_BPTPR=4 (curbele 2);
ρ_BPTPR=0.42 și I=5 (curbele 3);
ρ_BPTPR=0.42 și I=6; ρ_BPTPR=0.42 și I=7; I=4 și ρ=0.5 (curbele 4);
I=4 și ρ=0.58.
Cel mai bun rezultat: ρ=0.5 și I=4 (curbele 4).
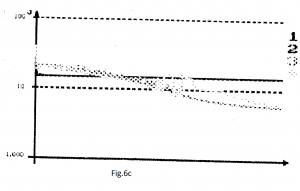
3). MULTIPLEXOR: ρ_BPTPR=0.98 și I=4 (curbele 1);
ρ_BPTPR=0.98 și I=5 (curbele 2);
ρ_BPTPR=0.98 și I=6 (curbele 3);
I=5 și ρ=1.06; I=5 și ρ=1.14; I=5 și ρ=1.22; I=5 și ρ=1.3 (curbele 4);
I=5 și ρ=1.38.
Cel mai bun rezultat: ρ=1.3 și I=5 (curbele 4).
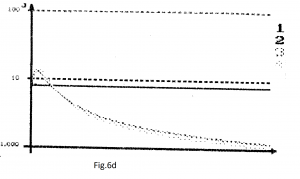
4). 5×5 TABLE: ρ_BPTPR=0.74 și I=2 (curbele 1);
ρ_BPTPR=0.74 și I=3 (curbele 2);
ρ_BPTPR=0.74 și I=4 (curbele 3);
ρ_BPTPR=0.74 și I_BPTPR=5; ρ_BPTPR=0.74 și I=6; I=3 și ρ=0.66; I=3 și ρ=0.82 (curbele 4).
Cel mai bun rezultat: ρ=0.74 și I=3 (curbele 2).

5). ASSOCIATIVE MEMORY: ρ_BPTPR=0.42 și I=4; ρ_BPTPR=0.42 și I=5 (curbele 1);
ρ_BPTPR=0.42 și I=6; ρ_BPTPR=0.42 și I=7 (curbele 2);
ρ_BPTPR=0.42 și I=8; ρ_BPTPR=0.42 și I=9; ρ_BPTPR=0.42 și I=10(curbele 3);
ρ_BPTPR=0.42 și I=11; I=10 și ρ=0.34; I=11 și ρ=0.5 (curbele 4).
Cel mai bun rezultat: ρ=0.42 și I=10 (curbele 3).
6). FUNCTION: ρ_BPTPR=0.02 și I=2 (curbele 1);
ρ_BPTPR=0.02 și I_BPTPR=3; I=2 și ρ=0.06; I=2 și ρ=0.1 (curbele 2);
I=2 și ρ=0.18; ρ=0.1 și I=3 (curbele 3);
ρ=0.1 și I=4; ρ=0.1 și I=5; ρ=0.1 și I=6 (curbele 4); ρ=0.1 și I=7.
Cel mai bun rezultat: ρ=0.1 și I=6 (curbele 4).

Observație: Comparând rezultatele obținute în variantele de învățare optime prin aceste 4 metode se observă în figura 7 (curba 1: BP; curba 2: BPTP; curba 3: BPTPR; curba 4: CGBP) superioritatea detașată a metodei CGBP. Situația apărută uneori (de exemplu, cazul problemei COUNTER) unde, deși pentru unele ponderi inițiale obținem rezultate foarte bune, uneori rezultatele sunt mai slabe ca la celelalte metode, apare din două motive:
a)complexitatea calculelor fiind mai mare, la același timp de rulare al algoritmului se execută mai puține iterații de învățare;
b)probabil că timpul de rulare a fost prea scurt pentru ca tendința descrescătoare a algoritmului CGBP să reușească să coboare funcția criteriu la valori mai mici.

3.5. BP and CGBP using the error’s absolute value minimization criterion

În toate exemplele prezentate aici, ponderile au fost calculate în termeni de eroare medie pătratică. Se prezintă următoarea problemă: care ar fi comportamentul rețelei dacă în loc de eroarea pătratică s-ar considera valoarea de eroare absolută? Am studiat această problemă în cazul a două metode de învățare: BP și CGBP, care s-au dovedit a fi cele mai bune.

Eroarea totală va fi calculată folosind aceeași formulă (3), dar $J_{s}^{\mu }$ , eroarea de ieșire absolută pentru modelul μ, va fi:

$J_{s}^{\mu }=\frac{1}{2}\cdot \sum_{m=1}^{M}\left | d_{m}^{\mu }- \mathfrak{F}\left ( a_{m}^{\mu } \right ) \right | (25)$

Unde, ca și în cazul precedent, d ^ μ este vectorul de ieșire dorit pentru clasa μ.

Urmând exact același raționament prezentat pe larg de formulele (5) – (10), vor rezulta relațiile de aplicat în acest caz:

$\Delta q_{mj}=\frac{\rho }{2}\cdot \sum_{\mu }\sigma \left [ d_{m}^{\mu}-\mathfrak{F(a_{m}^{\mu}}) \right ]\cdot\mathfrak{F(a_{m}^{\mu})}\cdot\frac{\partial a_{m}^{\mu}}{\partial q_{mj}}=\frac{\rho }{2}\cdot \sum_{\mu }\Delta _{m}^{\mu }\cdot v_{j}^{\mu } (26)$

$\Delta s_{m}= -\frac{\rho }{2}\sum_{\mu }\Delta _{m}^{\mu } (27)$

$\Delta _{m}^{\mu }=\sigma\left[d_{m}^{\mu}-\mathfrak{F(a_{m}^{\mu}})\right]\cdot\mathfrak{F(a_{m}^{\mu})}(28)$

Unde, prin σ[expresie] am considerat funcția care înapoiază semnul expresiei date.

Procedăm similar pentru parametrii alocați conexiunilor sinaptice dintre intrare și stratul ascuns:

$\Delta w_{ji}=\frac{\rho }{2}\cdot \sum_{\mu }\overline{\Delta}_{j}^{\mu }\cdot x_{i}^{\mu }(29)$

$\Delta c_{j}=\frac{\rho }{2}\cdot \sum_{\mu }\overline{\Delta }_{j}^{\mu } (30)$

$\overline{\Delta _{J}^{\mu }}=\left [ \sum_{m}^{ }\Delta _{m}^{\mu }\cdot q_{mj} \right ]\cdot \mathfrak{F(\overline{a_{j}^{\mu }})}(10)$

Extinzând la o rețea feed-forward cu R-straturi, criteriul de eroare care ar trebui minimizat este valoarea erorii absolute, determinată pe setul tuturor exemplelor de antrenare:

$J_{p}=\frac{1}{2}\cdot \sum_{\mu }\sum_{j_{1}=1}^{H_{1}}\left | d_{j_{1}}^{\mu }-v_{j_{1}}^{\mu } \right | (32)$

Expresiile (13-16) pot fi ușor modificate pentru cazul de față; modificarea majoră e legată de formula (15), care devine:

$\Delta _{j_{1}}^{\mu }=\sum_{j_{1}=1}^{H_{1}}\sigma \left [ d_{j_{1}}^{\mu }-\nu _{j_{1}}^{\mu } \right ]\cdot \mathfrak{F}\left ( \nu _{j_{1}}^{\mu } \right )(33))$

Pentru aceleași probleme pentru care au fost testate metodele de învățare anterioare, am rulat programe de simulare, iar rezultatele lor au fost reprezentate grafic, împreună cu cel mai bun rezultat obținut în cazul minimizării erorii pătratice. Spre deosebire de simulările anterioare, aici am folosit doar un set de ponderi inițiale și am păstrat pentru reprezentarea grafică doar cel mai bun rezultat. Acest fapt nu influențează concluziile finale privind compararea eficienței celor două metode, se poate vedea, în cele mai multe cazuri, superioritatea metodei folosind criteriul de minimizare a erorii pătratice față de a doua metodă.

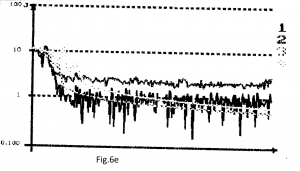
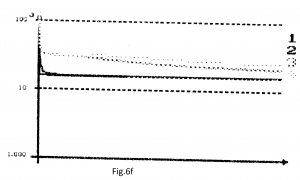
Pe fiecare din cele 6 grafice (fig.6a-6f), curbele 1 și 2 reprezintă cel mai bun rezultat obținut cu BP, respectiv metoda CGBP, folosind cel de-al doilea criteriu de minimizare a erorii; iar curbele 3 și 4 reprezintă cel mai bun rezultat după aplicarea acelorași metode de învățare (BP, respectiv CGBP), dar pentru primul criteriu de minimizare a erorii (minimizarea erorii pătratice).

Pentru metoda BP (curbele 1), am pornit inițial de la cea mai favorabilă valoare pentru ρ, pentru care am obținut cel mai bun comportament al rețelei, așa cum se arată la punctul 3. Am variat ρ până când s-a atins cel mai bun comportament pentru criteriul erorii absolute, s-a reprezentat grafic în curbele 1, acestea trebuie comparate cu curbele 3 (BP pentru criteriul erorii pătratice).

Pentru metoda CGBP (curbele 2), parametrii inițiali au fost: ρ optim găsit anterior și indicele optim de repornire I_{CGBP optim}, dar folosind metoda de eroare pătratică. Coeficientul ρ a fost menținut constant și indicele I a fost variat; apoi, după alegerea unui I optim, acesta a fost menținut constant și ρ a fost variat până când s-a atins cea mai potrivită valoare. Cu acești doi parametri cei mai buni, pentru fiecare aplicație au fost reprezentate graficele, curbele 2 trebuie comparate cu curbele 4.

Următoarele simulări au fost efectuate:

1). BINAR: BP: ρ=0.66 (curbele 1); CGBP: ρ=0.82, I=11 (curbele 2);BP: ρ=0.34 (curbele 3); CGBP: ρ=0.42, I=11 (curbele 4).

2). COUNTER: BP: ρ=0.5 (curbele 1); CGBP: ρ=0.5, I=4 (curbele 2);BP: ρ=0.5 (curbele 3); CGBP: ρ=0.42, I=4 (curbele 4).

3). MULTIPLEXOR: BP: ρ=1.22 (curbele 1); CGBP: ρ=1.22, I=5 (curbele 2);BP: ρ=1.22 (curbele 3); CGBP: ρ=1.3, I=5 (curbele 4).

4). 5X5 TABLE: BP: ρ=0.58 (curbele 1); CGBP: ρ=0.58, I=4 (curbele 2);BP: ρ=0.58 (curbele 3); CGBP: ρ=0.74, I=3 (curbele 4).

5). ASSOCIATIVE MEMORY: ρ=0.5 (curbele 1); CGBP: ρ=0.5, I=10 (curbele 2);BP: ρ=0.5 (curbele 3); CGBP: ρ=0.42, I=10 (curbele 4).

6).FUNCTION: BP: ρ=0.0005 (curbele 1); CGBP: ρ=0.5, I=10 (curbele 2);BP: ρ=0.02 (curbele 3); CGBP: ρ=0.1, I=6 (curbele 4).

4. O nouă metodă de tip BP (NBP)

Metodele cele mai populare de modificare a ponderilor rețelelor feedforward, respectiv metodele de tip backpropagation, sunt de fapt metode de gradient. Deoarece gradientul este o măsură locală, rezultă că pasul pe direcția gradientului, care pas este dat de rata de învățare ρ, trebuie să fie infinitezimal, ceea ce implică alegerea unui ρ foarte mic. Dar aceasta ar conduce la o convergență foarte înceată. De aceea, se alege totuși un ρ mai mare. Pe de altă parte, un ρ prea mare poate conduce la oscilații foarte mari ale funcției obiectiv. În plus, valorile lui ρ sunt relative la problema de rezolvat.
O soluție ar putea fi alegerea unui ρ oarecare și testarea lui pentru a vedea dacă produce oscilații și dacă da, atunci să se mai scadă valoarea lui până când nu mai avem oscilații. Cu alte cuvinte, am putea alege un ρ cât mai mare posibil fără apariția de oscilații. Dar acest tip de abordare conduce la un număr neprecizat de încercări pe un număr oarecare de iterații pentru a seta o valoare optimă a lui ρ. Ținând cont și de faptul că, după un număr oarecare de iterații se poate ajunge într-o regiune în spațiul ponderilor unde respectiva valoare să nu fie optimă, Silva și Almeida [16] au arătat avantajele alegerii unui pas independent pentru fiecare pondere în rețea. În algoritmul lor, rata de învățare se adaptează după fiecare pattern de antrenament:
$\rho _{ij}(k+1)=\left\{\begin{matrix} u\cdot \rho _{ij}(k), & daca\: \frac{\partial J_{k+1}}{\partial w_{ij}} si \frac{\partial J_{k}}{\partial w_{ij}} \: au \: acelasi \: semn\\ d\cdot \rho _{ij}(k),& daca\: \frac{\partial J_{k+1}}{\partial w_{ij}} si \frac{\partial J_{k}}{\partial w_{ij}} \: au \: semne\: diferite \end{matrix}\right.\; (25))$
unde u și d sunt constante pozitive: u puțin mai mare decât 1 (de exemplu 1,1) și d puțin mai mică decât 1 (de exemplu 0,9). Ideea este de a descrește rata de învățare la apariția oscilațiilor. S-au mai propus și alte metode la care pasul variază la fiecare iterație [6,9].
O soluție mai bună ar fi determinarea lui ρ la fiecare iterație. Deci, vom alege la fiecare iterație un pas cât mai mare posibil fără a avea oscilații. Vom genera o valoarea aleatorie a lui ρ, și vom determina, cu metoda gradienților conjugați cu restart, valorile ponderilor și vom testa măsura erorii J. Dacă eroarea este mai mică decât eroarea anterioară vom micșora ρ până când eroarea devine mai mică decât aceasta din urmă. În acest fel, dacă pe direcția gradientului eroarea totală scade, alegem pasul în acea direcție cât mai mare posibil; în caz contrar urmând să folosim proprietățile locale prin alegerea unui pas mic.
Prin posibilitatea de a alege pași oricât de mari se creează premisele evadării din minimele locale. Așadar, vom evada dintr-un minim local dacă pe direcția gradientului se găsește un minim ”mai minim” și întâmplător (datorită alegerii aleatorie a ρ-ului inițial) dăm peste el.
Deci, este foarte importantă alegerea ρ-ului inițial din fiecare iterație, care trebuie să fie suficient de mare pentru a putea evada din minimele locale, dar dacă este prea mare, atunci la fiecare iterație ar repeta pașii de micșorare a pasului. De aceea propun următoarea formulă [17] pe care am folosit-o în simulări:

ρ(k+1)=(1/2+ξ)∙ρ_mean ()∙(n_iterat+1) (35)
unde ξ este un număr uniform aleatoriu în intervalul (0,1), n_iterat este un întreg care indică de câte iterații criteriul J scade cu mai puțin de 1‰ și ρ_mean este media aritmetică a valorilor lui ρ din ultimele 10 iterații. Justificarea acestei formule este:
– ρ inițial trebuie să fie cel puțin 0,5;
– pentru a minimiza timpul de căutare al lui ρ final în fiecare iterație este de presupus că acesta va avea o valoare asemănătoare cu valorile anterioare, pentru că ”relieful” funcției criteriu J nu se schimbă substanțial dacă pașii exploatează proprietățile locale ale mediului. De aceea ρ inițial se determină ca media valorilor finale ale lui ρ în ultimele 10 iterații. Pentru calcului mediei eliminăm acele valorii care sunt prea mari sau prea mici în raport cu celelalte. La începutul învățării ρ_mean se setează la valoarea de 0.1. Astfel:
$\rho _{m(k)}=exp\left [ \frac{\sum_{i=1}^{10}ln(1+\rho (k-i+1))}{10} \right ]-1$
no_ρ ∶=10; ρ_sum ∶= 0;
for i:=1 to 10 do
if ((ρ(k-i+1) > ρ_m(k)/10) and (ρ(k-i+1) <10* ρ_m(k))
then ρ_sum:=ρ_sum+ρ(k-i+1)
else no_ρ:=no_ρ-1;
ρ_mean(k):=ρ_sum/no_ρ.
– dacă eroarea J nu scade de la o iterație la alta, înseamnă că suntem într-un minim local, din care ar fi bine să evadăm, așa că ar fi indicat să mărim ρ și de aceea apare ultimul factor. Mărimea inițială a lui ρ fiind stabilă, rămâne de fixat modalitatea de mărire și micșorare a ratei de învățare:
1). Determinăm cu algoritmul anterior un ρ inițial;
i:=0;
2). i:=i+1
3). Calculăm:
-variația ponderilor ∆w cu formula gradienților conjugați cu restart: (22) și
(24) unde I=5
-ponderile: w_k+1:=w_k+ρ∙∆w
-cu noile ponderi determinăm J₁
4). If J₁<J₀
Then Repeat
a). i:=i+1
b). Calculăm:
-variația ponderilor ∆w cu formula gradienților conjugați cu restart: (22) și (24)
-ponderile: w_k+1:=w_k+ρ∙u_i∙∆w
-cu noile ponderi determinăm J_i
Until J_i>J_i+1
w_k+1:=w_k+ρ∙u_i-1∙∆w
Else Repeat
a). i:=i+1
b). Calculăm:
-variația ponderilor ∆w cu formula gradienților conjugați cu restart
-ponderilor: w_k+1=w_k+(ρ/u_i )∙∆w
-cu noile ponderi determinăm Ji
Until J_i<J₀
w_k+1:=w_k+(ρ/u_i ) ∙∆w
5). Trecem la iterația următoare:
Șirul u_i poate fi șirul puterilor lui 2 (u_i=2ⁱ), dar noi preferăm șirul lui Fibonacci (1, 1, 2, 3, 5, 8, …), adică u_i = u_i-1+u_i+2, datorită bunelor rezultate obținute cu acesta și în teoria optimizării.
Se observă din grafice că, indiferent de tipul problemei, eroarea scade cu câteva ordine de mărime mai mult decât în celelalte metode ”clasice”. Chiar mai mult, eroarea evită (sau evadează) minimele locale, tinzând către eroarea 0 (minim absolut) pe care o și atinge uneori într-un număr mic de iterații.
Ar mai trebui justificat și de ce nu se micșorează ρ cât de mult posibil, așa cum se face atunci când se mărește, ci numai până când coboară sub valoarea inițială (din respectiva iterație) a erorii J. Nu caut să minimizez eroarea prin căutarea unui pas optim la fiecare iterație (ca la metodele de tip Newton-Raphson sau tip cvasi-Newton [1]) pentru că în acest fel am coborî foarte rapid (eventual într-o singură iterație) în cel mai apropiat minim local. Pentru evitarea minimelor locale preferăm o coborâre mai înceată și, în orice caz, prin pași cât mai mari posibili. Alegerea de pași mari (ρ mare) implică atât posibilitatea de a ”sări” în alte regiuni de minim, cât și salturi de o parte pe alta ”a gropii” (a ”văii”) în care se găsește minimul local, ceea ce conduce la modificarea direcției gradientului de la o iterație la alta. În acest fel, pe mai mute iterații se efectuează și o căutare, cu pași mari, în direcții diferite.
În figurile 8, 9, 10, 11, 12 și 13 am reprezentat rezultatele simulărilor pentru fiecare din cele 6 probleme în parte.
Curbele 1 reprezintă metoda clasică BP, curbele 2 metoda nouă propusă aici, iar curbele 3 metoda CGBP considerată ca cea mai bună dintre metodele testate anterior.
Superioritatea noii metode nu mai are nevoie de argumente. Este de remarcat totuși faptul că, chiar dacă maximul erorii din metoda NBP este uneori mai mare decât minimul erorii din celelalte metode, pentru fiecare set de ponderi inițiale eroarea NBP a fost cea mai mică față de eroarea la celelalte metode. Cu alte cuvinte, atunci când NBP ”merge rău”, celelalte metode ”merg și mai rău”.
De asemenea, utilizatorul nu este încărcat cu nicio sarcină de alegerea lui ρ sau, cum e în cazul CGBP (cea mai bună metodă clasică), și a lui I. Comportarea metodelor clasice este extrem de puternic influențată de alegerea acestor parametrii. La noua metodă nu mai este necesară nicio selecție preliminară a utilizatorului.

5. Concluzii
Metodele obișnuite de tip BP necesită efectuarea de testări pentru a determina valoarea optimă a lui ρ, valoare ce depinde de problema dată spre învățare. Metodele mai rafinate necesită și determinarea lui I.
Așadar, pe lângă convergența mai rapidă a metodei propuse, aceasta are și avantajul de a scuti utilizatorul de a efectua încercări preliminare pentru a determina pe ρ și pe I. Trebuie remarcat faptul că schimbările efectuate în programele de simulare la trecerea de la o metodă la alta au fost cât mai mici posibil, căutându-se să se modifice timpii de rulare numai pe baza creșterii complexității calculelor.
Cu toate că rețelele neurale sunt structuri tipic paralele, simularea s-a realizat pe un calculator și cu un algoritm secvențial. În cazul implementării unei structuri paralele, comparația ar trebui făcută nu la același timp de rulare, ci la același număr de iterații. Într-un asemenea caz, superioritatea metodei propuse NBP s-ar accentua.

6. Bibliografie

Battiti, R. ; Masulli, F. – ”BFGS Optimization for faster and automated supervised learning” – în “Proc. of the ICANN” – Espoo, Finlanda, iunie, 1991.
Benaim, M.; Tomasini, L. – “Competitive and self-organizing algorithms based on the minimisation of an information criteria” – în “Artificial Neural Networks”/ Kohonen, T.; Mkisara, K. ; Simula, O. ; Kanga, J.(Ed.) – Elsevier, Olanda, 1991.
Hornik, K. ; Stinchcombe, M. ; White, H. – “Multiplayer feedforward networks are universal approximators” – Neural Networks, nr.2 – 1989; pag. 359 – 366.
Hou, T. – H.; Lin, L. – “Manufacturing process monitoring using neural networks” – Computers & Elect. Engineering – Vol. 19, nr. 2, 1993 – pag. 129 – 141.
Hush, D.; Abdallah, C.; Horne, B. – “The recursive neural network and its applications in control theory” – Computer & Elect. Engineering – Vol. 19, nr. 4, 1993 –pag. 333-341.
Jacobs, R.A. – “Increased rates of convergence through learning rate adaptation” – Neural Networks – vol. 1, 1988 – pag. 295-307.
Krse, B.J.A.; Smagt, P.P. van der – “An Introduction to Neural Networks” – Universitatea din Amsterdam, 1993.
Narendra, K.; Parthasarathy, K. – “Identification and control of dynamical systems using neural networks” – IEEE Trans. On Neural Networks – Vol.1, nr. 1, 1990 – pag. 4-27.
Ooyen, A. van; Nienhuis, B. – “Improving the convergence of the back-propagation algorithm” – Neural Networks –vol.5, 1992 – pag.465-471.
Philips, S.; Wiles, J. – “Exponential generalization from a polynomial number of examples in a combinatorial domain” – în “Proceedings of the International Joint Conference on Neural Networks: IJCNN’93”- Nagoya, Japonia, octombrie, 1993, pag. 505-508.
Pineda, F. J. – “Generalization of backpropagation t recurrent and higher order neural networks” – în “Proceedings of IEEE Conference on Neural Information Processing Systems”/Anderson, D.Z. (Ed.) – Denver, CO – noiembrie, 1987.
Pineda, F.J. – “Dynamics and architecture for neural computation” – Journal of Complexity – nr. 4, 1988 – pag. 216-245.
Pineda, F.J. – “Recurrent backpropagation and the dynamical approach to adaptive neural computation” – Neural Computation – nr.1, 1989 – pag.161-172.
Pourboghrat, F. – “Adaptive neural controller design for robots” – Computers & Elect. Engineering – Vol.19, nr. 4, 1993 – pag. 277-288.
Ribar, S.; Koruga, D. – “Neural networks controller simulation” – în “Proc. of the ICANN” – Espoo, Finlanda, iunie, 1991.
Silva, F.M.; Almeida, L.B. – “Speeding up backpropagation” – în “Advanced neural computers”/Eckmiller, R (Ed.) – Olanda, 1990 – pag. 151-160.
Volovici, D. – “Fiabilitatea proceselor tehnologice flexibile” (Teză Doctorat) – Universitatea Politehnica București, Facultatea de Electronică și Telecomunicații, 1994.
Williams, R.J.; Zipser, D. – “A learning algorithm for continually running fully recurrent neural networks” – Neural Computation – nr.1; 1989, MIT – pag.270-280.